Assertions for IRV winners
In IRV elections, assertions are critical conditions used to verify that the announced winner truly won the election. Assertions allow us to narrow down the key elimination steps that need to be checked, rather than verifying every elimination order. There are two main types of assertions used in RAIRE: Not Eliminated Before (NEB) Assertions and Not Eliminated Next (NEN) Assertions.
Not Eliminated Before (NEB) Assertions
A Not Eliminated Before (NEB) assertion is a condition that states one candidate cannot be eliminated before another. This assertion allows us to focus on specific elimination orders and disregard paths that don’t affect the outcome. Alice NEB Bob is an assertion saying that Alice cannot be eliminated before Bob, irrespective of which other candidates are continuing. In other words, no outcome is possible in which Alice is eliminated before Bob.
When expressed as a comparison of tallies, this assertion says that the smallest number of votes Alice can have, at any point in counting, is greater than the largest number of votes Bob can ever have while Alice is continuing. Alice’s smallest tally is equal to her first preference count – the number of ballots on which she is ranked first. The largest number of votes Bob can have while Alice is continuing is the number of ballots on which he is ranked higher than Alice, or he is ranked and Alice is not.
Example
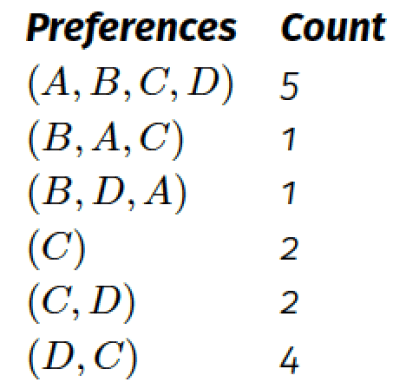
In the following example, Alice NEB Bob is true because Bob is ranked a total of 80 times without being preceded by Alice, which is less than Alice’s first-preference tally of 100. However, Alice NEB Diego is not true, because Diego is ranked 125 times without being preceded by Alice, which is more than Alice’s first preference tally.
Not Eliminated Next (NEN) Assertions
NEN assertions compare the tallies of two candidates under the assumption that a specific set of candidates have been eliminated. An instance of this kind of assertion could look like this: NEN: Alice > Bob if only {Alice, Bob, Diego} remain. This means that in the context where Chuan has been eliminated, Alice cannot be eliminated next, because Bob has a lower tally. When expressed as a comparison of tallies, this assertion says that the number of ballots in Alice’s tally pile, in the context where only Alice, Bob, and Diego are continuing, is greater than the number of ballots in Bob’s tally pile in this context.
This example assumes one eliminated candidate – Chuan – however, NEN assertions can be constructed with contexts involving no eliminated candidates, or more than one eliminated candidate. The assertion NEN: Alice > Chuan if only {Alice, Bob, Chuan, Diego} remain says that Alice cannot be the first eliminated candidate, as she has more votes than Chuan when no candidates have yet been eliminated. The assertion NEN: Diego > Bob if only {Bob, Diego} remain says that Diego has more votes than Bob in the context where those two are the only continuing candidates.
Simple assertions sometimes work
RAIRE works by generating a set of assertions which, together, imply a particular winner. In this section, we introduce some common patterns that those sets of assertions might use. We aim to make it obvious why certain sets of assertions are enough to imply a particular winner, and to match a person’s intuition about why a certain candidate won an IRV election.
One candidate dominates
Sometimes one candidate happens to be so strongly ahead of all the others that NEB assertions hold with all other candidates.
Example
Suppose that for the four candidates Alice, Bob, Chuan, and Diego, we have:
Alice NEB Bob,
Alice NEB Chuan and
Alice NEB Diego.
Two leading candidates
Now suppose there are two candidates who accumulate most of the votes: Alice and Bob.
Example
Suppose Alice NEB Bob is not true, but the following weaker fact is true:
NEN: Alice > Bob if only {Alice, Bob} remain.
This says that, after Chuan and Diego are eliminated, Alice’s tally is higher than Bob’s.
Assume we still have two NEB assertions:
Alice NEB Chuan
and
Alice NEB Diego.
This, again, is enough to prove that Alice won. To see why, consider the last elimination step. Alice must reach this step, because she cannot have been eliminated before Chuan or Diego. If Chuan or Diego is the other remaining candidate, Alice beats them (by the NEB assertion). The only other possibility is Bob—for this case, the NEN assertion shows that, in the last round, Alice beats Bob.
Visualizing assertions
This reasoning can be visualized using elimination trees. For an audit, we need to disprove all elimination orders that result in a winner other than the announced winner.
The assertion Alice NEB Chuan is enough to disprove every elimination order in which Alice is eliminated before Chuan, and hence to disprove the entire tree in which Chuan wins. It also allows us to disprove the orders in Bob’s tree and Diego’s tree in which Alice is eliminated before Chuan.
The consequences of Alice NEB Chuan in Bob’s tree and Chuan’s tree are shown below. It still allows the possibility that Bob might win via elimination orders Diego, Chuan, Alice, Bob, or Chuan, Diego, Alice, Bob, or Chuan, Alice, Diego, Bob.


By sharing your files or using our service, you agree to our Terms of Service and Privacy Policy.
